Viscosity coefficients can be defined in two ways:. Dynamic viscosity, also absolute viscosity, the more usual one (typical units Pas, Poise, P);. Kinematic viscosity is the dynamic viscosity divided by the density (typical units m2/s, Stokes, St). Viscosity Charts & Conversion Tables DAIRY PRODUCTS ButterFat 42 110 ButterFat 20 150 ButterDeodorized 45 120 CottageCheese 30,000 65 CocoaButter 50 140 CocoaButter 0.5 210 CondensedMilk 40–80 100–120 CondensedMilk,75%Solids 2,160 70 Cream,30%Fat 14 60 Cream,45%Fat 48 60 Cream,50%Fat 112 60 Cream,50%Fat 55 90 Milk 2.0 65 Milk 10 120.
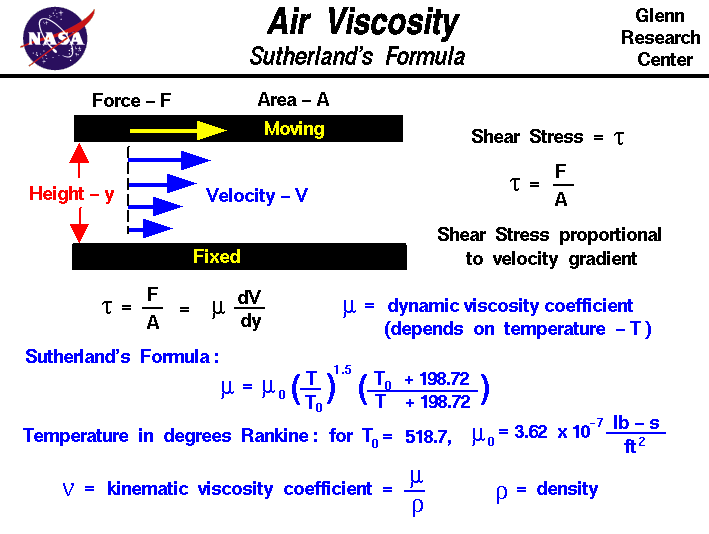
Where u is the viscosity; b is a constant (1.458 x 10^-6) T is the temperature (Kelvin) S is another constant (110.4) Viscosity of Air Definition. The viscosity of air is defined as the air gasses’ resistance to flow and is dependent solely on the temperature. Viscosity of Air Example. The viscosity of air, at atmospheric pressure is the following: Air viscosity at 0°c = 0.01722 mPa.s Air viscosity at 25°c = 0.0186 mPa.s 2.
The absolute viscosity of many fluids relatively doesn't change with the pressure but very sensitive to temperature. For isothermal flow, the viscosity can be considered constant in many cases. The variations of air and water as a function of the temperature at atmospheric pressure are plotted in Figures 1.8 and 1.9.
Some common materials (pure and mixture) have expressions that provide an estimate. For many gases, Sutherland's equation is used and according to the literature, provides reasonable of (-40°C) to (1600°C). [mu = mu_{0} frac{0.555 T_{i0} + Suth}{0.555 T_{in} + Suth} (frac{T}{T_0})^frac{3}{2}]
Where
(mu) viscosity at input temperature, T
(mu_{0}) reference viscosity at reference temperature, (T_{i0})
(T_{in}) input temperature in degrees Kelvin
(T_{i0}) reference temperature in degrees Kelvin
(Suth) Sutherland's constant (presented in Table 1.1)
Example 1.3
Calculate the viscosity of air at 800K based on Sutherland's equation. Use the data provide in Table 1.1.
Solution 1.3
Applying the constants from Suthelnd's table provides
[ mu = 0.00001827 times dfrac{ 0.555times524.07+120}{0.555times800+120} times left( dfrac{800}{524.07}right)^{dfrac{3}{2}} sim 2.51,{10}^{-5} left[dfrac{N, sec}{m^2}right] ]
The observed viscosity is about (sim 3.7{10}^{-5}left[dfrac{N, sec}{m^2}right]).
Table 1.2 Viscosity of selected gases.
| Substance | Chemical formula | Temperature, (T,[^{circ}C]) | Viscosity, (left[dfrac{N, sec}{m^2} right]) |
| (i-C_4,H_{10}) | 23 | 0.0000076 | |
| (CH_4) | 20 | 0.0000109 | |
| Oxygen | (O_2) | 20 | 0.0000203 |
| Mercury Vapor | (Hg) | 380 | 0.0000654 |
Table 1.3 Viscosity of selected liquids.
| Substance | Chemical formula | Temperature, (T,[^{circ}C]) | Viscosity, (left[dfrac{N, sec}{m^2} right]) |
| ((C_2H_5)O) | 20 | 0.000245 | |
| (C_6H_6) | 20 | 0.000647 | |
| (Br_2) | 26 | 0.000946 | |
| (C_2H_5OH) | 20 | 0.001194 | |
| (Hg) | 25 | 0.001547 | |
| (H_2SO_4) | 25 | 0.01915 | |
| Olive Oil | 25 | 0.084 | |
| Castor Oil | 25 | 0.986 | |
| Clucuse | 25 | 5-20 | |
| Corn Oil | 20 | 0.072 | |
| SAE 30 | - | 0.15-0.200 | |
| SAE 50 | (sim25^{circ}C) | 0.54 | |
| SAE 70 | (sim25^{circ}C) | 1.6 | |
| Ketchup | (sim20^{circ}C) | 0,05 | |
| Ketchup | (sim25^{circ}C) | 0,098 | |
| Benzene | (sim20^{circ}C) | 0.000652 | |
| Firm glass | - | (sim 1times10^7) | |
| Glycerol | 20 | 1.069 |
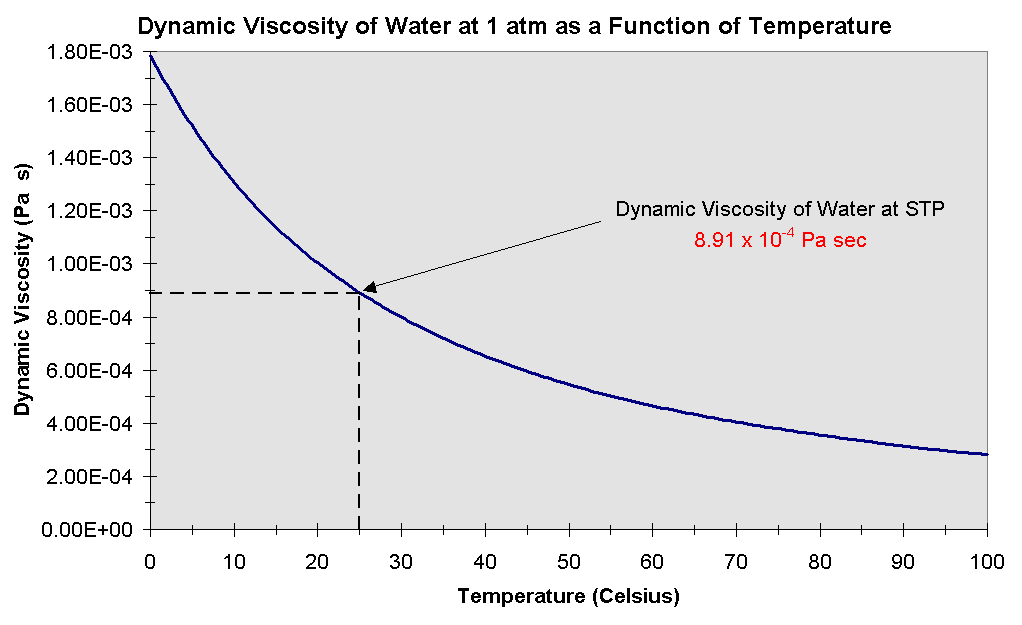
Fig. 1.10. Liquid metals' viscosity as a function of the temperature.
Liquid Metals
Liquid metal can be considered as a Newtonian fluid for many applications. Furthermore, many aluminum alloys are behaving as a Newtonian liquid until the first solidification appears (assuming steady state thermodynamics properties). Even when there is a solidification (mushy zone), the metal behavior can be estimated as a Newtonian material (further reading can be done in this author's book ``Fundamentals of Die Casting Design'). Figure 1.10 exhibits several liquid metals (from The Reactor Handbook, Vol. Atomic Energy Commission AECD-3646 U.S. Government Printing Office, Washington D.C. May 1995 p. 258.)
The General Viscosity Graphs
In case ``ordinary' fluids where information is limit, Hougen et al suggested to use graph similar to compressibility chart. In this graph, if one point is well documented, other points can be estimated. Furthermore, this graph also shows the trends. In Figure 1.11 the relative viscosity (mu_{r} = mu / mu_{c}) is plotted as a function of relative temperature, (T_{r}). (mu_{c}) is the viscosity at critical condition and (mu) is the viscosity at any given condition. The lines of constant relative pressure (P_{r} = P / P_{c}) are drawn. The lower pressure is, for practical purpose, (sim1[bar]).
Table 1.3 Viscosity of selected liquids.
| Chemical component | Molecular Weight | (T_c)[K] | (P_c)[Bar] | (mu_c)(left[dfrac{N,sec}{m^2}right]) |
| (H_2) | 2.016 | 33.3 | 12.9696 | 3.47 |
| (He) | 4.003 | 5.26 | 2.289945 | 2.54 |
| (Ne) | 20.183 | 44.5 | 27.256425 | 15.6 |
| (Ar) | 39.944 | 151 | 48.636 | 26.4 |
| (Xe) | 131.3 | 289.8 | 58.7685 | 49. |
| Air 'mixed' | 28.97 | 132 | 36.8823 | 19.3 |
| (CO_2) | 44.01 | 304.2 | 73.865925 | 19.0 |
| (O_2) | 32.00 | 154.4 | 50.358525 | 18.0 |
| (C_2H_6) | 30.07 | 305.4 | 48.83865 | 21.0 |
| (CH_4) | 16.04 | 190.7 | 46.40685 | 15.9 |
| Water | 18.01528 | 647.096 K | 22.064 [MPa] | ∼ 11. |
The critical pressure can be evaluated in the following three ways. The simplest way is by obtaining the data from Table 1.4 or similar information. The second way, if the information is available and is close enough to the critical point, then the critical viscosity is obtained as [mu_{c} = frac{mu}{mu_{r}}] The third way, when none is available, is by utilizing the following approximation [mu_{c} = sqrt{MT_{c}}v_{c}^{2/3}] Where ___vc with sim hat___ is the critical molecular volume and (M) is molecular weight. Or [mu_{c} = sqrt{M}P_{c}^{2/3}T_{c}^{-1/6}] Calculate the reduced pressure and the reduced temperature and from the Figure 1.11 obtain the reduced viscosity.
Example 1.4
Estimate the viscosity of oxygen, (O_2) at (100^{circ}C) and 20[Bar].
Solution 1.4
(P_c = 50.35[Bar],) (T_c=154.4) and therefore (mu_c=18 left[ dfrac{N,sec}{m^2}right]) The value of the reduced temperature is
[left[ dfrac{N,sec}{m^2}right] ]
[P_r sim dfrac{20}{50.35} sim 0.4 ]From Figure 1.11 it can be obtained (mu_rsim 1.2) and the predicted viscosity is
[mu = mu_c , overbrace{left( dfrac{mu}{mu_c}right)}
^{Table } = 18 times 1.2 = 21.6[N sec/m^2] ]
Fig. 1.11. Reduced viscosity as a function of the reduced temperature.
Fig. 1.12. Reduced viscosity as a function of the reduced temperature.
Viscosity of Mixtures
In general the viscosity of liquid mixture has to be evaluated experimentally. Even for homogeneous mixture, there isn't silver bullet to estimate the viscosity. In this book, only the mixture of low density gases is discussed for analytical expression. For most cases, the following Wilke's correlation for gas at low density provides a result in a reasonable range. [mu_{mix} = sum_{i=1}^n frac{x_{i}mu_{i}}{sum_{j=1}^n x_{i}phi_{ij}}] where (phi_{ij}) is defined as [phi_{ij} = frac{1}{sqrt{8}}sqrt{1+frac{M_i}{M_j}}(1+sqrt{frac{mu_i}{mu_j}}{frac{M_j}{M_i})^2)
Here,
(n) the number of the chemical components in the mixture
(x_{i}) is the mole fraction of component (i)
mu_{i} the viscosity of component (i)
The subscript (i) should be used for the (j) index.
The dimensionless parameter (phi_{ij})
is equal to one when (i=j). The mixture viscosity is highly nonlinear function of the fractions of the components.
Example 1.5
Calculate the viscosity of a mixture (air) made of 20% oxygen, (O_2) and 80% nitrogen (N_2) for the temperature of (20^{circ}C).
Solution 1.5
The following table summarizes the known details
Table summary 1.
| Component | Molecular Weight, (M) | Fraction, (x) | Viscosity, (mu) |
| (O_2) | 32. | 0.2 | 0.0000203 |
| (N_2) | 28. | 0.8 | 0.00001754 |
Table summary 2.
| i | j | (M_i/M_j) | (mu_i/mu_j) | (Phi_{ij}) |
| 1 | 1 | 1.0 | 1.0 | 1.0 |
| 1 | 2 | 1.143 | 1.157 | 1.0024 |
| 2 | 1 | 0.875 | .86 | 0.996 |
| 2 | 2 | 1.0 | 1.0 | 1. |
[ mu_{mix} sim dfrac{0.2times 0.0000203}{0.2times1.0 + 0.8times 1.0024} + dfrac{0.8times 0.00001754}{0.2times0.996 + 0.8times 1.0} sim 0.0000181 left[dfrac{N,sec}{m^2}right] ]
The observed value is (sim0.0000182 left[dfrac{N,sec}{m^2}right]).
In very low pressure, in theory, the viscosity is only a function of the temperature with a ``simple' molecular structure. For gases with very long molecular structure or complexity structure these formulas cannot be applied. For some mixtures of two liquids it was observed that at a low shear stress, the viscosity is dominated by a liquid with high viscosity and at high shear stress to be dominated by a liquid with the low viscosity liquid. The higher viscosity is more dominate at low shear stress. Reiner and Phillippoff suggested the following formula:
[frac{dU_{x}}{dy} = left(frac{1}{mu_{infty} + frac{mu_{0} - mu_{infty}}{1 + (frac{tau_{xy}}{tau_{s}})^2}}right)tau_{xy}]
Where the term (mu_{infty}) is the experimental value at high shear stress. The term (mu_0) is the experimental viscosity at shear stress approaching zero. The term (tau_s) is the characteristic shear stress of the mixture. An example for values for this formula, for Molten Sulfur at temperature (120^{circ}C) are (mu_{infty} = 0.0215 left({N,sec}/{m^2}right)), (mu_{0} = 0.00105 left({N,sec}/{m^2}right)), and (tau_s = 0.0000073 left({kN}/{m^2}right)). This equation (29) provides reasonable value only up to (tau = 0.001 left({kN}/{m^2}right)).
Figure 1.12 can be used for a crude estimate of dense gases mixture. To estimate the viscosity of the mixture with (n) component Hougen and Watson's method for pseudocritial properties is adapted. In this method the following are defined as mixed critical pressure as
[{P_c}_{mix} = sum_{i=1}^{n} , x_i ,{P_c}_i ]
[{T_c}_{mix} = sum_{i=1}^{n} ,x_i, {T_c}_i ]and the mixed critical viscosity is
[{mu_c}_{mix} = sum_{i=1}^{n} ,x_i, {mu_c}_i ]
Example 1.6
Fig. 1.13 Concentrating cylinders with the rotating inner cylinder.
of 0.101 [m] radius and the cylinders length is 0.2 [m]. It is given that a moment of 1 [(Ntimes m)] is required to maintain an angular velocity of 31.4 revolution per second (these number represent only academic question not real value of actual liquid). Estimate the liquid viscosity used between the cylinders.}
Solution 1.6
The moment or the torque is transmitted through the liquid to the outer cylinder. Control volume around the inner cylinder shows that moment is a function of the area and shear stress. The shear stress calculations can be estimated as a linear between the two concentric cylinders. The velocity at the inner cylinders surface is [ label{concentricCylinders:Ui} U_i = r,omega = 0.1times 31.4[rad/second] = 3.14 [m/s] ] The velocity at the outer cylinder surface is zero. The velocity gradient may be assumed to be linear, hence, [ label{concentricCylinders:dUdr} dfrac{dU}{dr} cong dfrac{0.1- 0}{0.101 - 0.1} = 100 sec^{-1} ] The used moment is [ label{concentricCylinders:M1} M = overbrace{2,pi,r_i,h}^{A} overbrace{mu dfrac{dU}{dr}}^{tau} ,overbrace{r_i}^{ll} ] or the viscosity is [ label{concentricCylinders:M} mu = dfrac{M}{ {2,pi,{r_i}^2,h} { dfrac{dU}{dr}} } = dfrac{1}{2timespitimes{0.1}^2 times 0.2 times 100} = ]
Example 1.7
A square block weighing 1.0 [kN] with a side surfaces area of 0.1 [(m^2)] slides down an incline surface with an angle of 200C. The surface is covered with oil film. The oil creates a distance between the block and the inclined surface of (1times10^{-6}[m]). What is the speed of the block at steady state? Assuming a linear velocity profile in the oil and that the whole oil is under steady state. The viscosity of the oil is (3 times 10^{-5} [m^2/sec]).
Solution 1.7
The shear stress at the surface is estimated for steady state by [ label{slidingBlock:shear} tau = mu dfrac{dU}{dx} = 3 times 10^{-5} times dfrac{U}{1times10^{-6}} = 30 , U ] The total fiction force is then [ label{slidingBlock:frictionForce} f = tau, A = 0.1 times 30,U = 3,U ] The gravity force that acting against the friction is equal to the friction hence [ label{slidingBlock:solPre1} F_g = f = 3,ULongrightarrow U = dfrac{m,g,sin,20^{circ}}{3} ] Or the solution is [ label{slidingBlock:solPre} U = dfrac{1times 9.8timessin,20^{circ}}{3} ]
Example 1.8
Fig. 1.14 Rotating disc in a steady state.
The edge effects can be neglected. The gap is given and equal to (delta) and the rotation speed is (omega). The shear stress can be assumed to be linear.}
Solution 1.8
In this cases the shear stress is a function of the radius, (r) and an expression has to be developed. Additionally, the differential area also increases and is a function of (r). The shear stress can be estimated as [ label{discRotating:tau} tau cong mu ,dfrac{U}{delta} = mu,dfrac{omega , r}{delta} ] This torque can be integrated for the entire area as [ label{discRotating:F} T = int_0^R r, tau ,dA = int_0^R overbrace{r}^{ll} , overbrace{mu, dfrac{omega , r}{delta}}^{tau} , overbrace{2,pi,r,dr}^{dA} ] The results of the integration is [ label{discRotating:I} T = dfrac{pi,mu,omega,R^4}{2,delta} ]
Viscosity Of Air 25c
Contributors and Attributions
Dr. Genick Bar-Meir. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or later or Potto license.
Atmospheric air is a mixture of nitrogen and oxygen being the earth atmosphere. Main components of air which are practically the same throughout the globe are nitrogen (78.08 volume per cent) and oxygen (20.95 v.%). Along with them air contains 0.94 v.% of inert gases and 0.03 v.% of carbon dioxide. The air of such a composition is named dry. Its molecular mass is regarded to be M = 28.96 g/mole.
In the lower atmosphere strata the air contains also water vapor, its concentration is substantially variable depending on the partial water vapor pressure at the appropriate temperature and relative humidity. For instance at 20°C and relative humidity 80% air contains about 0.02 v.% of water vapor. In the air layers adjacent to the earth surface other components may be present being in most cases of antropogenic origin.
At ambient pressure and temperature air can be regarded as a perfect gas, its properties may be described by equations:
where v denotes specific volume; u is specific internal energy; R is the gas constant for air.
At low temperatures the air is liquified. The normal (at 0.1013 MPa) boiling (condensation) temperature of the oxygen is equal— 183°C, that of the nitrogen -195.8°C. Liquid air at atmospheric pressure behaves practically as an ideal solution following the Raoult's Law. The normal condensation temperature of air is -191.4°C, the normal boiling temperature -194°C.
At elevated temperatures air undergoes some physicochemical transformations. The nitrogen reacts with oxygen producing various oxides: N2O, NO, NO2, NO3. Their equilibrium concentration can be derived from the isotherm equations of the respective reactions.
At temperatures higher than 2000 K and moderate pressures the nitrogen and oxygen start to dissociate, and at temperatures exceeding 4000 K and atmospheric pressure the ionization of oxygen, nitrogen, and other components becomes evident. This implies the transition of air into the plasma state. The equilibrium dissociation degree can be calculated according to the Saha equation.
The thermodynamic properties of air along the saturation curve are given in Table 1; these properties for the liquid and gaseous air—in Table 2.
Table 1. Thermodynamic properties of air along the saturation curve
Viscosity Of Air 70f
Table 2. Thermodynamic properties of liquid and gaseous air
The enthalpy is taken as zero at an arbitrary point. The entropy is taken zero for the solid air at 0K.
Air is a mixture mainly consisting of diatomic gases. Therefore its heat capacity at close to normal temperatures and pressures may with good accuracy be taken equal to
where
With increasing temperature the heat capacity slightly increases due to exciting of the vibrational degrees of freedom in the oxygen and nitrogen molecules. Table 3 gives air heat capacity values for a wide range of temperatures and pressures.
Table 3. Air heat capacity cp, KJ/kg · K
As for all pure substances in the supercritical region, the isobars and isotherms of the heat capacity cp have maximums the steeper the closer to the critical point.

The temperature dependence of the viscosity of air is qualitatively the same as for pure substances: in the liquid phase the viscosity decreases with temperature following an approximately exponential function; in the gas phase at low pressures the viscosity increases according to equation:
with increasing pressure at constant temperature the viscosity increases. This dependence is most strong in the vicinity of the critical point. Air viscosity values at various temperatures and pressures are given in Table 4.
Table 4. Air viscosity η · 107, N · s/m2
The behavior of the thermal conductivity of air is similar to the viscosity: in the liquid phase with growing temperature the heat conductivity decreases whereas in the gas phase-increases. At low pressures the temperature dependence is described by the equation:
Viscosity Of Air 80f
Along the isotherm with increasing pressure the thermal conductivity increases. In Table 5 the air thermal conductivity is given at various temperatures and pressures.
Table 5. Air thermal conductivity λ · 103, W/m · K
At low pressures and high temperatures the thermal conductivity sharply increases due to dissociation. With growing temperature the thermal conductivity goes through maximums which are connected with maximum heat transfer by the heats of respective reactions. Thermal conductivities of air at dissociation conditions are given in Table 6.
Table 6. Air thermal conductivity at high temperatures λ · 103, W/m · K
Viscosity Of Air English Units
REFERENCES
Additional information about air properties can be found in the following literature: Handbook, edited by V. P. Glushko (1978) 'Nauka' Publishing House, Moskow (in Russian).
Wassermann, A. A. and Rabinovitch, V. A. (1968) Thermophysical properties of liquid air and its components. Standarts Publishing House, Moscow (in Russian).
Handbook Thermophysical Properties of Gases and Liquids, edited by N. B. Vargaftic (1972) 'Nauka' Publishing House, Moscow (in Russian).
References
- Additional information about air properties can be found in the following literature: Handbook, edited by V. P. Glushko (1978) 'Nauka' Publishing House, Moskow (in Russian).
- Wassermann, A. A. and Rabinovitch, V. A. (1968) Thermophysical properties of liquid air and its components. Standarts Publishing House, Moscow (in Russian).
- Handbook Thermophysical Properties of Gases and Liquids, edited by N. B. Vargaftic (1972) 'Nauka' Publishing House, Moscow (in Russian).